Grandissement Optique d'un Objectif d'Imagerie

Jeudi 3 octobre 2024

Grandissement optique, distance et angle de champ

Il est bien connu que le grandissement optique d'un objectif d'imagerie change avec la distance de l'objet (distance entre l'objet et l'objectif). Cependant, il est moins connu que le grandissement optique d'un objectif d'imagerie change également avec l'angle de champ (c'est-à-dire l'endroit où l'objet est placé dans le champ).

Grandissement optique asymétrique

En outre, le grandissement optique hors axe peut être asymétrique. En d'autres termes, les grandissements optiques tangentiel et sagittal peuvent être différents. Cela entraîne une déformation de la forme des objets hors axe. Par exemple, une balle de golf hors axe peut avoir une image de forme ovale. Dans cet article, nous abordons les concepts de "grandissement relatif" et de "rapport d'aspect" utiles pour caractériser la déformation de la forme des objets hors axe. La compréhension de ce sujet aidera à optimiser la conception des lentilles pour les applications d'apprentissage machine (machine learning).

Pour un objet sur l'axe situé à l'infini, la taille de l'image est le produit de la distance focale effective de l'objectif (EFL) et de l'angle (en radians) sous-tendu par l'objet depuis la position de la pupille d'entrée. Lorsque cet objet est déplacé hors axe, la taille de l'image dépend de la fonction de représentation de l'objectif h(θ), où h est la hauteur de l'image sur le plan de l'image et θ est l'angle de champ.  La dérivée dh/dθ fournit le grandissement tangentiel (ou méridional). Les définitions de l'orientation tangentielle et sagittale sont illustrées par cette figure.

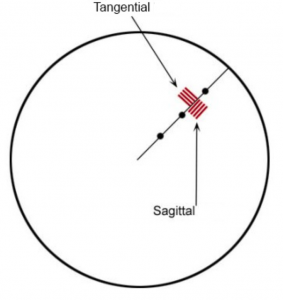
Grandissement optique tangentiel relatif

Nous pouvons définir le grandissement tangentiel relatif comme étant le grandissement tangentiel divisé par le grandissement sur l'axe. Dans le cas particulier où la fonction de représentation de l'objectif est simplement EFL*θ, le grandissement tangentiel est une constante, indépendante de l'angle du champ (mais le grandissement sagittal ne l'est pas). Un tel objectif est appelé objectif f-θ. D'autres formes bien connues de fonction de représentation des lentilles comprennent : rectiligne, stéréographique, angle équisolide et orthographique (voir cet article de Wikipedia :https://fr.wikipedia.org/wiki/Objectif_fisheye). 

Rectilinéarité concept de Sunex

Il convient de noter que la plupart des objectifs du monde réel ne suivent pas ces équations avec précision. Sunex a développé un concept appelé "rectilinéarité" comme paramètre généralisé pour caractériser l'ensemble des fonctions de représentation des objectifs. Veuillez nous contacter si vous souhaitez en savoir plus à ce sujet. 

La plupart des lentilles optiques sur le marché aujourd'hui ont une symétrie axiale. Sur la base de cette symétrie, on peut montrer que le grandissement optique sagittal est h(θ)/sin(θ). Le grandissement sagittal relatif est défini comme le grandissement sagittal divisé par le grandissement sur l'axe pour les systèmes à symétrie axiale. Le rapport entre le grandissement tangentiel relatif et le grandissement sagittal relatif est alors défini comme le "rapport d'aspect". Si le rapport d'aspect est de 1 à tous les angles de champ, la forme de l'objet est invariante dans le champ de vision de l'objectif. Un tel objectif peut contribuer à améliorer la précision des algorithmes d'apprentissage machine.

Etudes de cas

Étudions quelques cas particuliers :

• Le type le plus courant de fonction de représentation des lentilles optiques est dit rectiligne. La fonction de représentation est basée sur un modèle de trou minuscule (pinhole) où la hauteur de l'image est proportionnelle à la tangente de l'angle de champ. Les exemples de lentilles optiques rectilignes comprennent la plupart des lentilles optiques photographiques, y compris celles des smartphones. Les grandissements tangentiels et sagittaux relatifs augmentent avec l'angle de champ, mais pas à la même vitesse. L'augmentation tangentielle est plus rapide, ce qui donne un rapport d'aspect qui augmente également avec l'angle de champ. L'effet en pratique est qu'une personne proche du bord horizontal est étirée dans le sens de la largeur.
• Un objectif « angle fidèle » (stéréographique) : le grandissement tangentiel et sagittal augmente avec l'angle de champ, mais à la même vitesse. Le rapport d'aspect est invariant dans le champ de vision d'un objectif stéréographique.
• Un objectif f-θ a un grandissement tangentiel constant. Cependant, le grandissement sagittal augmente avec l'angle du champ. Par conséquent, le rapport d'aspect diminue lorsque l'angle du champ augmente. Les objets hors axe deviennent "allongés" sagittalement.
• Une lentille à « angle fidèle » (equisolid angle) a un grandissement tangentiel décroissant mais un grossissement sagittal croissant, le produit des deux étant constant. Bien que les objets hors axe soient déformés, ils occupent approximativement le même nombre de pixels dans le plan image. Si l'algorithme d'apprentissage machine nécessite un nombre minimum de pixels dans le champ de vision pour fonctionner, un objectif à « angle fidèle » peut être utile.

Pour plus de renseignements sur les solutions en imagerie proposée par Optics Concept, n'hésitez pas à les contacter !

Sources :

https://en.wikipedia.org/wiki/Magnification
https://en.wikipedia.org/wiki/Fisheye_lens#Mapping_function
https://fr.wikipedia.org/wiki/Objectif_fisheye